图 | 二二八

图论基础

邻接表&邻接矩阵

出度、入度等基础概念自行百度.

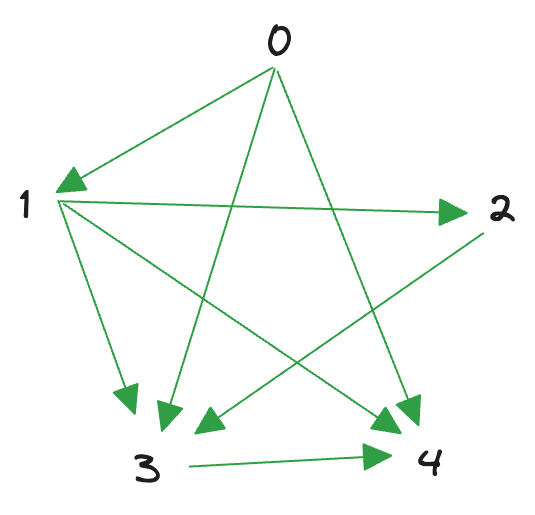
上面这幅有向图，分别用邻接表和邻接矩阵实现如下：

// 邻接表，当然也可以用 hashmap 来实现
const graph: Array<number[]> = [[1, 3, 4], [2, 3, 4], [3], [4], []]
// 邻接矩阵，当然元素不仅仅只能为 Boolean 值
const graph: Array<boolean[]> = [
  [false, true, false, true, true],
  [false, false, true, true, true],
  [false, false, false, true, false],
  [false, false, false, false, true],
  [false, false, false, false, false],
]

邻接表：占用空间少；判断两个节点是否相邻，需要遍历所有相邻的节点
邻接矩阵：存在很多空洞，占用空间大；判断两个节点是否相邻简单，获取 matrix[i][j] 的值即可

图的遍历

图的遍历，需要注意的是图可能有环：

必须要有 visited 变量来防止走入死循环
遍历过程中可以使用 onPath 变量判断当时的路径是否成环（类比贪吃蛇蛇身）

/** visited 类似贪吃蛇走过的所有路径；onPath 类似设蛇身 */
// 记录所有遍历过的节点
const visited = []
// 记录从起点到当前节点的路径
const onPath = []

/* 图遍历框架 DFS */
function traverse(graph, s) {
  if (visited[s]) return
  // 经过节点 s，标记为已遍历
  visited[s] = true
  // 做选择：标记节点 s 在路径上
  onPath[s] = true
  for (const neighbor of graph.neighbors(s)) {
    traverse(graph, neighbor)
  }
  // 撤销选择：节点 s 离开路径
  onPath[s] = false
}

回溯做选择和撤销选择是在 for 循环内，对应选择、撤销选择的对象是「树枝」
DFS 做选择和撤销选择是在 for 循环外，对应选择、撤销选择的对象是「节点」
抽象出「树枝，节点」是为了更加形象的理解，其实放在 for 循环外就是为了不要漏掉「初始节点」。具体的请参看暴力递归-DFS&回溯这篇文章。

lc.797 所有可能的路径

var allPathsSourceTarget = function (graph) {
  // 有向无环图, graph 的 index 自身即为 node; graph[index] 为邻居
  let res = []
  const onPath = []
  const dfs = (node) => {
    onPath.push(node)
    if (node === graph.length - 1) {
      res.push([...onPath])
      /** 因为无环，所以不用 return；如果 return 同时需要维护 onPath */
      // onPath.pop()
      // return
    }
    for (let i = 0; i < graph[node].length; ++i) {
      dfs(graph[node][i])
    }
    onPath.pop()
  }
  dfs(0)
  return res
}

经典问题

有向图环检测&拓扑排序

对于有「依赖关系」的问题，一般可以抽象为一副有向图，检测是否有循环依赖即可。

lc.207 课程表

用邻接表的形式来抽象本题的有向图。

dfs 检测环，借助图遍历中的 onPath 数组，判断蛇身是否相撞即可

/**
 * @param {number} numCourses
 * @param {number[][]} prerequisites
 * @return {boolean}
 */
var canFinish = function (numCourses, prerequisites) {
  // 先构图
  const graph = Array.from(Array(numCourses), () => [])
  for (let i = 0; i < prerequisites.length; ++i) {
    const [to, from] = prerequisites[i]
    graph[from].push(to) // from -> to
  }
  // 再判断是否有环
  const onPath = [] // 记录遍历过程
  const visited = [] // 防止进入死循环
  let hasCycle = false
  const dfs = (node) => {
    // 蛇身成环
    if (onPath.indexOf(node) > -1) {
      hasCycle = true
      return
    }
    if (visited.indexOf(node) > -1 || hasCycle) return
    onPath.push(node)
    visited.push(node)
    for (const neighbor of graph[node]) {
      dfs(neighbor)
    }
    onPath.pop()
  }

  for (let i = 0; i < numCourses; ++i) {
    dfs(i)
  }
  return !hasCycle
}

bfs 检测环，需要借助入度数组，当某个节点入度为 0 的时候代表它成为了头了，加入队列

/**
 * @param {number} numCourses
 * @param {number[][]} prerequisites
 * @return {boolean}
 */
var canFinish = function (numCourses, prerequisites) {
  // 先构图 + 构建入度数组
  const graph = Array.from(Array(numCourses), () => [])
  const indegree = Array(numCourses).fill(0)
  for (let i = 0; i < prerequisites.length; ++i) {
    const [to, from] = prerequisites[i]
    graph[from].push(to) // from -> to
    indegree[to]++
  }
  // 寻找入度为 0 的节点加入队列，然后开始 bfs 遍历
  const queue = []
  for (let i = 0; i < numCourses; ++i) {
    indegree[i] === 0 && queue.push(i)
  }
  let visitedCount = 0
  while (queue.length) {
    // 这道题不用向四周分散，而是去操作入度数组
    visitedCount++
    const node = queue.shift()
    const indegreeOfNode = graph[node]
    for (let i = 0; i < indegreeOfNode.length; ++i) {
      indegree[indegreeOfNode[i]]--
      if (indegree[indegreeOfNode[i]] === 0) {
        queue.push(indegreeOfNode[i])
      }
    }
  }

  // 如果所有节点都被遍历过，说明不成环
  // 1. 如果就是一个完整环，那么没有入度为 0 的节点不会进入遍历
  // 2. 如果是图中有一部分为环，那么环起点的入度始终不会为 0
  return visitedCount === numCourses

lc.210 课程表 II

此题相比上一题，无非就是需要记录下来完整的依赖图，那么就得了解下「拓扑排序了」：拓扑排序-维基百科

直观点讲，就是把一幅有向图拉平后，每条边的指向相同。

dfs 拓扑：在上一题 dfs 检测环的后续位置收集节点为一个集合，对这个集合逆序即为拓扑排序的一个结果；或者在构图时，graph[to].push(from)，最后就不用逆序了

// 1. 要实现拓扑排序，图不能有环，因为要确保每条边 u 在 v 之前 // 2. 有向无环图的拓扑排序至少有一种 // 3. dfs 和 bfs 都能实现拓扑排序 // 3.1 DFS 算法利用逆后序遍历（或者利用逆邻接表）进行拓扑排3.2 序，BFS 借助 indegree(入度) 数组也能实现。

/**
 * @param {number} numCourses
 * @param {number[][]} prerequisites
 * @return {number[]}
 */
var findOrder = function (numCourses, prerequisites) {
  const graph = Array.from(Array(numCourses), () => [])
  for (let i = 0; i < prerequisites.length; ++i) {
    const [to, from] = prerequisites[i]
    graph[to].push(from) // 注意这里！
  }
  let res = []
  let hasCycle = false
  const visited = []
  const onPath = []
  const dfs = (node) => {
    if (onPath.indexOf(node) > -1) {
      hasCycle = true
      return
    }
    if (visited.indexOf(node) > -1 || hasCycle) return
    onPath.push(node)
    visited.push(node)
    for (const neighbor of graph[node]) {
      dfs(neighbor)
    }
    res.push(node)
    onPath.pop()
  }
  for (let i = 0; i < numCourses; ++i) {
    dfs(i)
  }
  if (hasCycle) return []
  return res
}

bfs 拓扑：在上一题 bfs 检测环的基础上，很容易理解出队的顺序就是拓扑排序的结果。

var findOrder = function (numCourses, prerequisites) {
  // 先构图 + 构建入度数组
  const graph = Array.from(Array(numCourses), () => [])
  const indegree = Array(numCourses).fill(0)
  for (let i = 0; i < prerequisites.length; ++i) {
    const [to, from] = prerequisites[i]
    graph[from].push(to) // from -> to
    indegree[to]++
  }
  // 寻找入度为 0 的节点加入队列，然后开始 bfs 遍历
  const queue = []
  for (let i = 0; i < numCourses; ++i) {
    indegree[i] === 0 && queue.push(i)
  }
  let visitedCount = 0
  const res = []
  while (queue.length) {
    // 这道题不用向四周分散，而是去操作入度数组
    visitedCount++
    const node = queue.shift()
    res.push(node)
    const indegreeOfNode = graph[node]
    for (let i = 0; i < indegreeOfNode.length; ++i) {
      indegree[indegreeOfNode[i]]--
      if (indegree[indegreeOfNode[i]] === 0) {
        queue.push(indegreeOfNode[i])
      }
    }
  }
  if (visitedCount !== numCourses) return []
  return res
}

从检测环的角度来说：「拓扑排序」可以判断-有向图-是否有环，「并查集」可以判断-无向图-是否有环

并查集

参考了此篇文章 https://oi-wiki.org/ds/dsu/

并查集通常用来解决「连通性」问题 --- 主要功能大白话就是：

Union - 将两个元素合并到一个集合中
Find - 判断两个元素是否在同一个集合里

如何让两个元素连通呢？father[a] = b; father[b] = c，这样就好了，通过 a 可以找到 b，通过 b 可以找到 c。

基础

并查集的实现为一个森林（多个树），每个树表示一个集合，树的每个节点表示一个元素。

/** disjoint sets union */
class Dsu {
  // 初始化：每个元素位于一个「单独的集合」，--根节点为自身--
  constructor(size) {
    this.father = Array.from(Array(size), (_, index) => index)
  }
  // 把集合 u, v 合并到一个集合，合并的是根~
  join(u, v) {
    u = find(u) // 寻根
    v = find(v) // 寻根
    if (u === v) return
    this.father[v] = u // 请注意！：这里连通的是入参 u，v 的根
  }
  // 向上寻根
  find(u) {
    if (u === this.father[u]) return u // 自身
    // return find(this.father[u])
    /**
     * 路径压缩： 如果每次都如上行那样递归寻找上级，比较浪费时间
     * 路径压缩就是把节点直接接到根节点上，而这一步操作可以巧妙的在 find 过程中完成，如下：
     */
    return (this.father[u] = find(this.father[u]))
  }
}

启发式合并：

上面的合并比较随意，合并时，选择哪棵树的根节点作为新树的根节点会影响未来操作的复杂度。我们可以将节点较少或深度较小的树连到另一棵。将较小集合合并到较大集合有助于平衡树的高度，从而提高查询效率。

// constructor
this.size = Array(size).fill(1)

union(u, y) {
    u = this.find(u);
    v = this.find(v);
    if (u === v) return
    if (this.size[u] < this.size[v]) {
        [u, v] = [v, u];
    }
    this.father[v] = u;
    this.size[u] += this.size[v];
}

练习

lc.684 冗余连接

检测无向图的环~ 思想也很简单，利用并查集的 find，当新加入的边如果找到了同一个根，则说明新加入的边使得原来的树形成了环；否则就 union 新加入的边即可。

/**
 * @param {number[][]} edges
 * @return {number[]}
 */
var findRedundantConnection = function (edges) {
  const len = edges.length
  const DSU = Array.from(Array(len + 1), (_, index) => index)
  for (let i = 0; i < len; ++i) {
    const [u, v] = edges[i]
    const u1 = find(DSU, u)
    const v1 = find(DSU, v)
    if (u1 === v1) return edges[i]
    DSU[v1] = u1 // union 简化到这里
  }
  return [0]
}
function find(p, u) {
  if (u === p[u]) return u
  return (p[u] = find(p, p[u]))
}

lc.130 被围绕的区域

/**
 * @param {character[][]} board
 * @return {void} Do not return anything, modify board in-place instead.
 */
var solve = function (board) {
  if (board.length === 0) return
  // 这道题一看就是岛屿类的问题，自然可以用 flood fill 算法去搞定，但本次重点是并查集~
  const rowLen = board.length
  const colLen = board[0].length

  const DSU = Array.from(Array(rowLen * colLen + 1), (_, index) => index) // 多一个最后的节点用于给 dummyNode
  const dummyNode = rowLen * colLen // 如果不用 dummyNode 就略微复杂了

  // 遍历四条件边，把四条边上的 O 与 dummyNode 连通
  for (let i = 0; i < rowLen; ++i) {
    if (board[i][0] === 'O') union(DSU, i * colLen, dummyNode)
    if (board[i][colLen - 1] === 'O') union(DSU, i * colLen + colLen - 1, dummyNode)
  }
  for (let j = 0; j < colLen; ++j) {
    if (board[0][j] === 'O') union(DSU, j, dummyNode)
    if (board[rowLen - 1][j] === 'O') union(DSU, (rowLen - 1) * colLen + j, dummyNode)
  }

  // 遍历整个内部节点，把所有的 O 连通起来（连完后，如果和边缘连接的就会在一个集合，否则在另一个集合）
  // 利用方向数组遍历上下左右
  const dirs = [
    [-1, 0],
    [1, 0],
    [0, -1],
    [0, 1],
  ]
  for (let i = 1; i < rowLen - 1; ++i) {
    for (let j = 1; j < colLen - 1; ++j) {
      if (board[i][j] === 'O') {
        for (const [x, y] of dirs) {
          const nx = i + x
          const ny = j + y
          if (board[nx][ny] === 'O') {
            union(DSU, i * colLen + j, nx * colLen + ny)
          }
        }
      }
    }
  }
  // 遍历整个 board， 把中间包围的且没有和 dummyNode 连通的 O 变为 X
  for (let i = 1; i < rowLen - 1; ++i) {
    for (let j = 1; j < colLen - 1; ++j) {
      if (board[i][j] === 'O' && find(DSU, i * colLen + j) !== find(DSU, dummyNode)) {
        board[i][j] = 'X'
      }
    }
  }
}
function find(p, u) {
  if (u === p[u]) return u
  return (p[u] = find(p, p[u]))
}
function union(p, u, v) {
  u = find(p, u)
  v = find(p, v)
  if (u === v) return
  p[v] = u
}

简单说一下，用 flood fill 算法怎么做，也很简单，就是先 dfs 四条边，先把与边相连的 O 都标记上，最后对整个 board 遍历，把 O 转为 x，把标记的转回为 O 即可。 lc.200 & lc.1905 与本题类似，之前用的 dfs flood fill 算法去做的，有时间可以用 DSU 也做一做。

这是不使用虚拟节点的并查集，就得需要维护 isEdge 来标记是否与边缘相连了

class UnionFind {
  constructor(n) {
    this.parent = new Array(n).fill(null).map((_, idx) => idx)
    this.isEdge = new Array(n).fill(false) // 标记是否与边缘相连
  }

  find(x) {
    if (this.parent[x] !== x) {
      this.parent[x] = this.find(this.parent[x])
    }
    return this.parent[x]
  }

  union(x, y) {
    let rootX = this.find(x)
    let rootY = this.find(y)

    if (rootX !== rootY) {
      this.parent[rootY] = rootX
      // 更新rootX的边缘状态
      this.isEdge[rootX] = this.isEdge[rootX] || this.isEdge[rootY]
    }
  }
}

/**
 * @param {character[][]} board
 * @return {void} Do not return anything, modify board in-place instead.
 */
var solve = function (board) {
  if (board.length === 0) {
    return
  }

  const rows = board.length
  const cols = board[0].length
  const uf = new UnionFind(rows * cols)

  // 定义边界条件
  const isEdge = (i, j) => i == 0 || i == rows - 1 || j == 0 || j == cols - 1

  // 遍历矩阵中所有的'O'节点
  for (let i = 0; i < rows; i++) {
    for (let j = 0; j < cols; j++) {
      if (board[i][j] === 'O') {
        let idx = i * cols + j
        // 如果是边缘节点，则将其标记为与边缘相连
        uf.isEdge[idx] = isEdge(i, j)

        // 将当前'O'节点与相邻的'O'节点进行连接
        let neighbors = [
          [i + 1, j],
          [i - 1, j],
          [i, j + 1],
          [i, j - 1],
        ]
        for (let [ni, nj] of neighbors) {
          if (ni >= 0 && ni < rows && nj >= 0 && nj < cols && board[ni][nj] === 'O') {
            uf.union(idx, ni * cols + nj)
          }
        }
      }
    }
  }

  // 遍历矩阵，将不与边缘相连的'O'节点改为'X'
  for (let i = 0; i < rows; i++) {
    for (let j = 0; j < cols; j++) {
      if (board[i][j] === 'O' && !uf.isEdge[uf.find(i * cols + j)]) {
        board[i][j] = 'X'
      }
    }
  }
}

lc.990 等式方程的可满足性

知道用并查集的前提下，这还不是小 case~ 又是一个无向图检测环的问题罢了。

/**
 * @param {string[]} equations
 * @return {boolean}
 */
var equationsPossible = function (equations) {
  // 很明显的环检测问题
  const DSU = Array.from(Array(26), (_, index) => index)
  for (let i = 0; i < equations.length; ++i) {
    const edge = equations[i]
    const isConnected = edge[1] === '='
    if (isConnected) {
      const u = edge.charCodeAt(0) - 'a'.charCodeAt()
      const v = edge.charCodeAt(3) - 'a'.charCodeAt()
      union(DSU, u, v)
    }
  }
  for (let i = 0; i < equations.length; ++i) {
    const edge = equations[i]
    const isNotConnected = edge[1] === '!'
    if (isNotConnected) {
      const u = edge.charCodeAt(0) - 'a'.charCodeAt()
      const v = edge.charCodeAt(3) - 'a'.charCodeAt()
      if (find(DSU, u) === find(DSU, v)) return false
    }
  }
  return true
}
function find(p, u) {
  if (u === p[u]) return u
  return (p[u] = find(p, p[u]))
}
function union(p, u, v) {
  u = find(p, u)
  v = find(p, v)
  if (u === v) return
  p[v] = u
}